Introduction to Stack in Data Structures and Algorithms
Introduction :
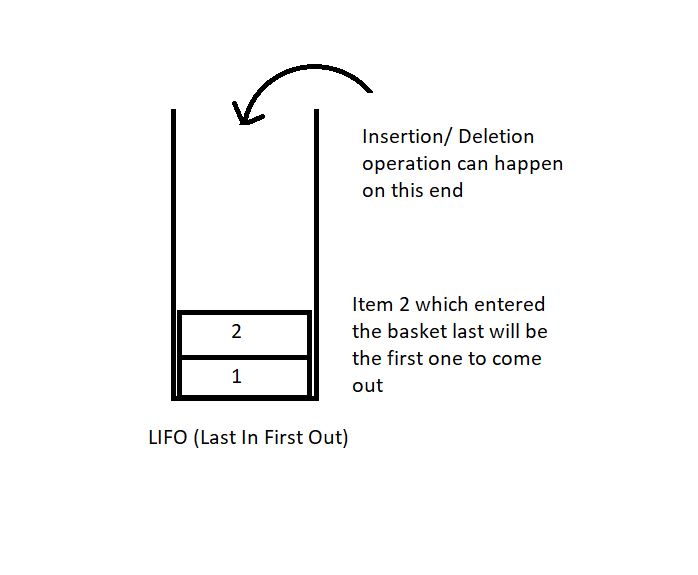
A stack is a linear data structure. Any operation on the stack is performed in LIFO (Last In First Out) order. This means the element to enter the container last would be the first one to leave the container. It is imperative that elements above an element in a stack must be removed first before fetching any element.
An element can be pushed in this basket-type container image below. Any basket has a limit, and so does our container too. Elements in a stack can only be pushed to a limit. And this extra pushing of elements in a stack leads to stack overflow.
Applications of Stack:
A function until it returns reserves a space in the memory stack. Any function embedded in some function comes above the parent function in the stack. So, first, the embedded function ends, and then the parent one. Here, the function called last ends first. (LIFO).
Infix to postfix conversion (and other similar conversions) will be dealt with in the coming tutorials.
Parenthesis matching and many more...
**Stack ADT:
**In order to create a stack, we need a pointer to the topmost element to gain knowledge about the element which is on the top so that any operation can be carried about. Along with that, we need the space for the other elements to get in and their data.
Here are some of the basic operations we would want to perform on stacks:
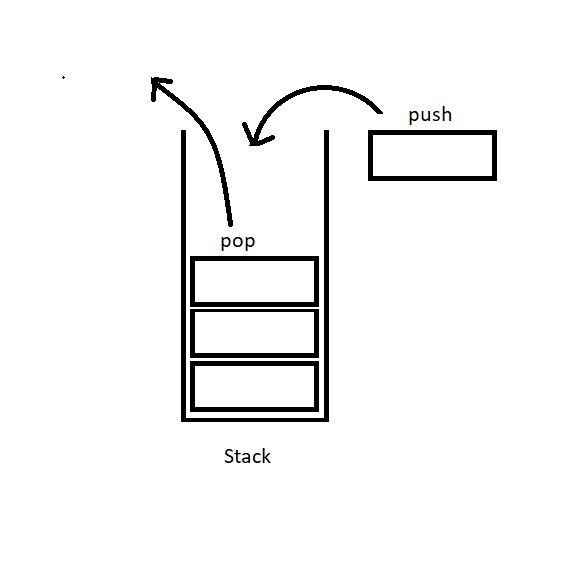
push(): to push an element into the stack
pop(): to remove the topmost element from the stack
peek(index): to return the value at a given index
isempty() / isfull() : to determine whether the stack is empty or full to carry efficient push and pull operations.
Implementing Stack Using Array
Stack Using an Array
If we recall, arrays are linear data structures whose elements are indexed, and the elements can be accessed in constant time with their index. To implement a stack using an array, we’ll maintain a variable that will store the index of the top element.
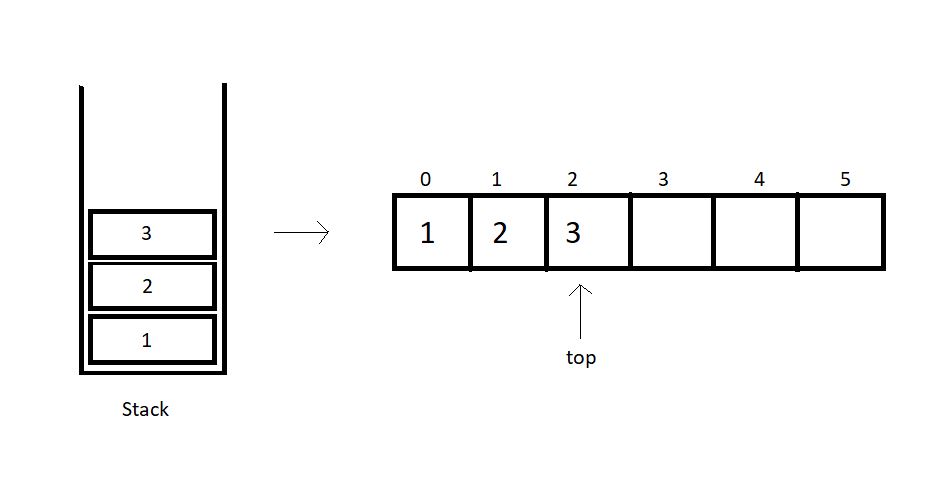
So, basically, we have few things to keep in check when we implement stacks using arrays.
1. A fixed-size array. This size can even be bigger than the size of the stack we are trying to implement, to stay on the safe side.
2. An integer variable to store the index of the top element, or the last element we entered in the array. This value is -1 when there is no element in the array.
We will try constructing a structure to embed all these functionalities. Let’s see how.
struct stack
{
int size;
int top;
int* arr;
}
So, the struct above includes as its members, the size of the array, the index of the top element, and the pointer to the array we will make.
To use this struct,
You will just have to declare a struct stack
Set its top element to -1.
Furthermore, you will have to reserve memory in the heap using malloc.
Follow the example below for defining a stack:
struct stack S;
S.size = 80;
S.top = -1;
S.arr = (int*)malloc(S.size*sizeof(int));
We have used an integer array above, although it is just for the sake of simplicity. You have the freedom to customize your data types according to your needs.
We can now move on implementing the stack ADT, particularly their operators. We have in the list, push and pull, peek, and isempty/full operation. Let’s visit them one by one.
push():
By pushing, we mean inserting an element at the top of the stack. While using the arrays, we have the index to the top element of the array. So, we’ll just insert the new element at the index (top+1) and increase the top by 1. This operation takes a constant time, O(1). It’s intuitive to note that this operation is valid until (top+1) is a valid index and the array has an empty space.
pop():
Pop means to remove the last element entered in the stack, and that element has the index top. So, this becomes an easy job. We’ll just have to decrease the value of the top by 1, and we are done. The popped element can even be used in any way we like.
C Code For Implementing Stack Using Array
1. So, the first thing would be to create the struct Stack we discussed in the previous tutorial. Include three members, an integer variable to store the size of the stack, an integer variable to store the index of the topmost element, and an integer pointer to hold the address of the array.
struct stack
{
int size;
int top;
int *arr;
};
2. In main, create a struct stack s, and assign a value 80(you can assign any value of your choice) to its size, -1 to its top, and reserve memory in heap using malloc for its pointer arr. Don’t forget to include <stdlib> .
3. We have one more method to declare these stacks. We can define a struct stack pointer s, and use the arrow operators to deal with their members. The advantage of this method is that we can pass these pointers as references into functions very conveniently.
4. Before we advance to pushing elements in this stack, there are a few conditions to deal with. We can only push an element in this stack if there is some space left or the top is not equal to the last index. Similarly, we can only pop an element from this stack if some element is stored or the top is not equal to -1.
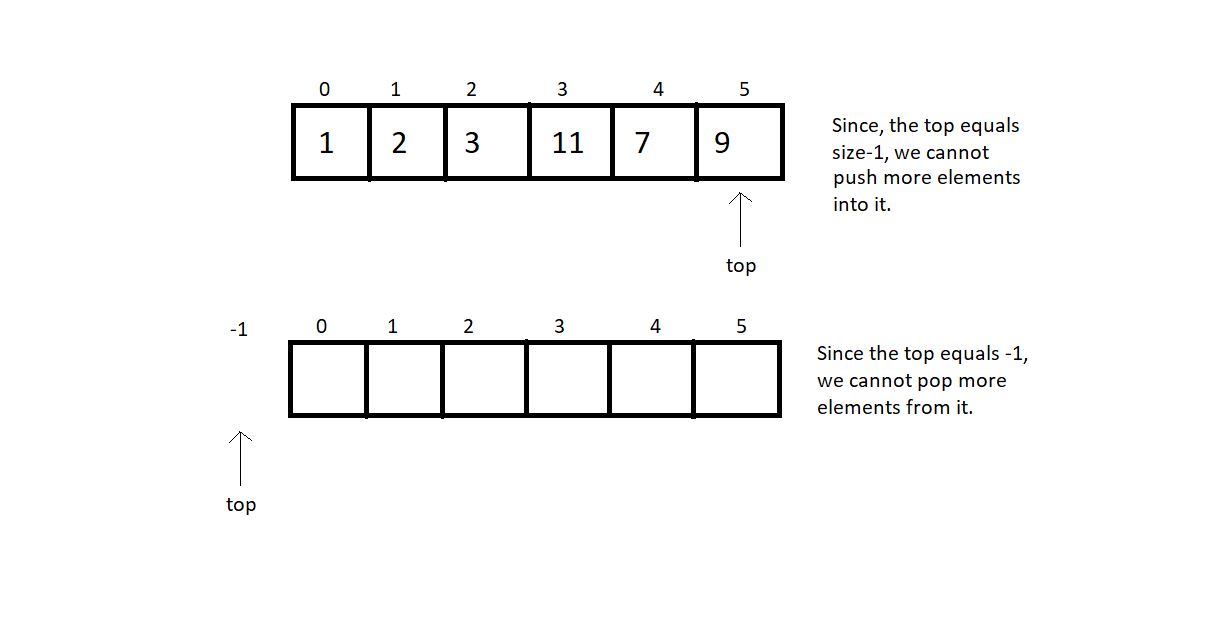
5. So, let us first write functions to check whether these stacks are empty or full.
6. Create an integer function isEmpty, and pass the pointer to the stack as a parameter. In the function, check if the top is equal to -1. If yes, then it’s empty and returns 1; otherwise, return 0.
int isEmpty(struct stack *ptr)
{ if (ptr->top == -1)
{
return 1;
}
else
{
return 0;
}
}
7. Create an integer function isFull, and pass the pointer to the stack as a parameter. In the function, check if the top is equal to (size-1). If yes, then it’s full and returns 1; otherwise, return 0.
int isFull(struct stack *ptr)
{
if (ptr->top == ptr->size - 1)
{
return 1;
}
else
{
return 0;
}
}
Implementing isFull
Push, Pop and Other Operations in Stack Implemented Using an Array
We had already finished the basics of a stack, and its implementation using arrays. We have gained enough confidence by writing the codes for implementing stacks using arrays in C. Now we can learn about the operations one can perform on a stack while executing them using arrays.
We concluded our last tutorial with two of the most important points:
One cannot push more elements into a full-stack.
One cannot pop any more elements from an empty stack.
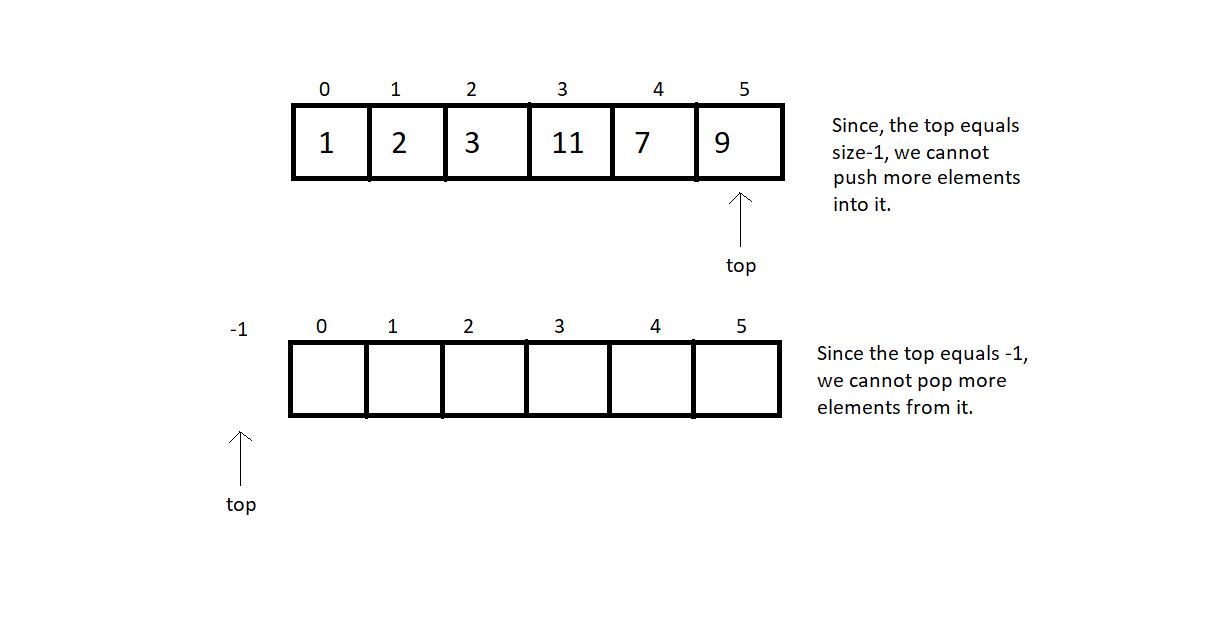
Declaring a stack was done in the last tutorial as well. Let's keep that in mind as we proceed.
Operation 1: Push-
1. The first thing is to define a stack. Suppose we have the creating stack and declaring its fundamentals part done, then pushing an element requires you to first check if there is any space left in the stack.
2. Call the isFull function which we did in the previous tutorial. If it’s full, then we cannot push anymore elements. This is the case of stack overflow. Otherwise, increase the variable top by 1 and insert the element at the index top of the stack.
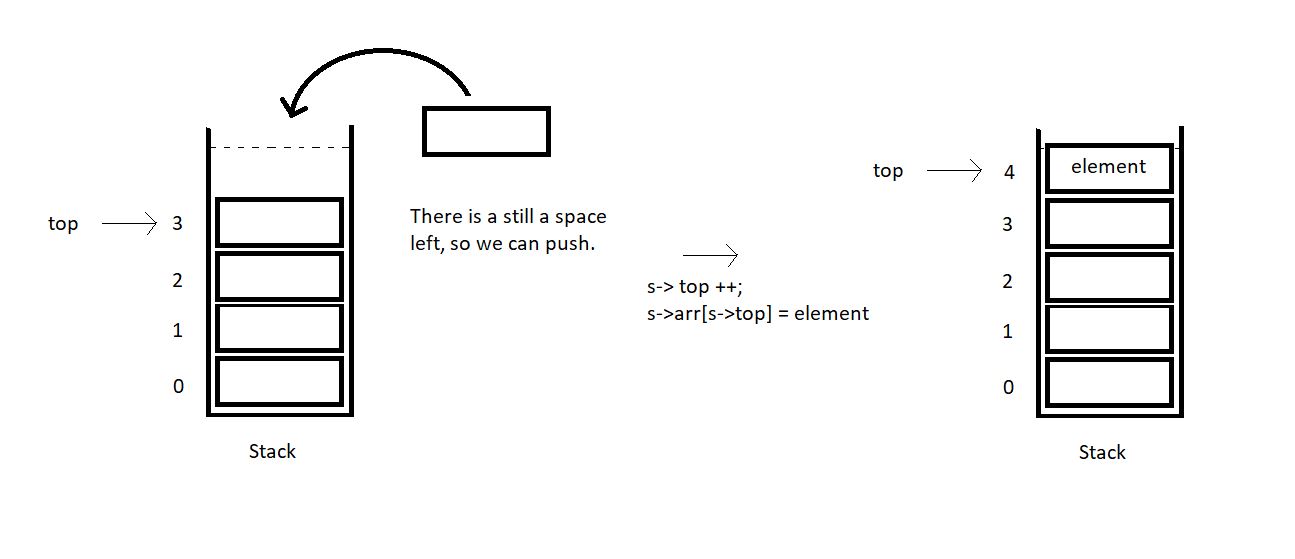
3. So, this is how we push an element in a stack array. Suppose we have an element x to insert in a stack array of size 4. We first checked if it was full, and found it was not full. We retrieved its top which was 3 here. We made it 4 by increasing it once. Now, just insert the element x at index 4, and we are done.
Operation 2: Pop-
Popping an element is very similar to inserting an element. You should first give it a try yourself. There are very subtle changes.
1. The first thing again is to define a stack. Get over with all the fundamentals. You must have learnt that by now. Then popping an element requires you to first check if there is any element left in the stack to pop.
2. Call the isEmpty function which we practiced in the previous tutorial. If it’s empty, then we cannot pop any element, since there is none left. This is the case of stack underflow. Otherwise, store the topmost element in a temporary variable. Decrease the variable top by 1 and return the temporary variable which stored the popped element.
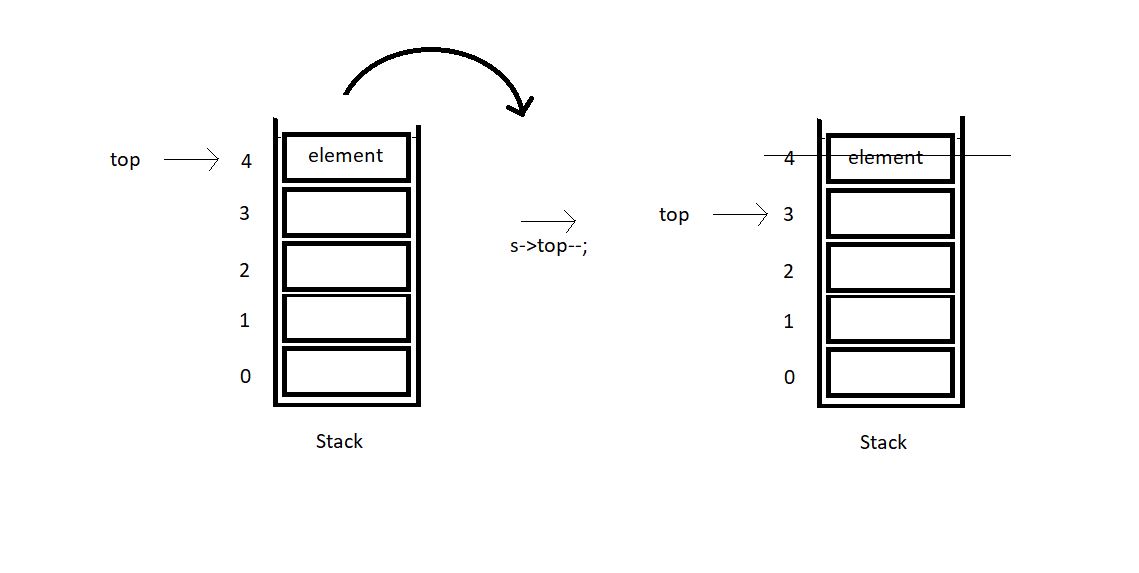
3. So, this is how we pop an element from a stack array. Suppose we make a pop call in a stack array of size 4. We first checked if it was empty, and found it was not empty. We retrieved its top which was 4 here. Stored the element at 4. We made it 3 by decreasing it once. Now, just return the element x, and popping is done.
Peek Operation in Stack Using Arrays
Peek operation requires the user to give a position to peek at as well. Here, position refers to the distance of the current index from the top element +1.
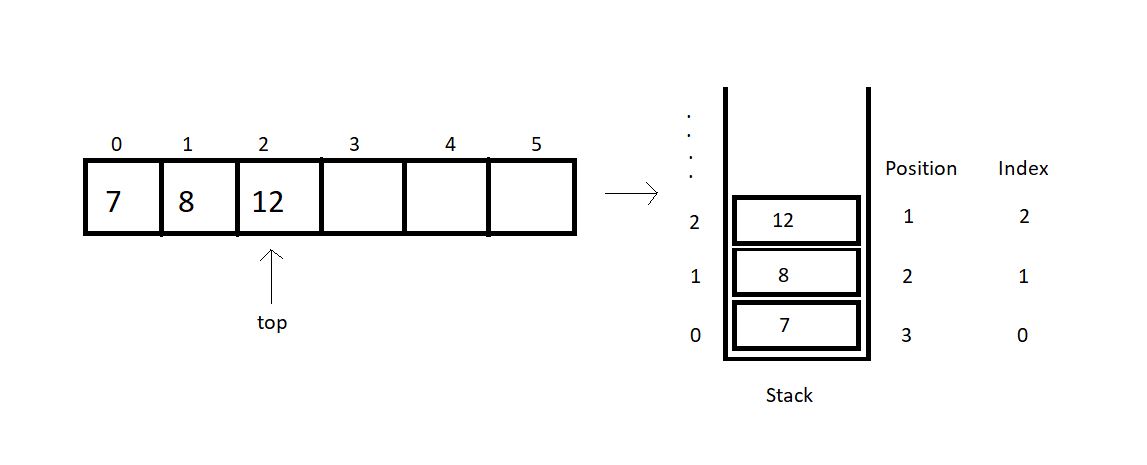
The index, mathematically, is (top -position+1).
So, before we return the element at the asked position, we’ll check if the position asked is valid for the current stack. Index 0, 1 and 2 are valid for the stack illustrated above, but index 4 or 5 or any other negative index is invalid.
Note: peek(1) returns 12 here.
Now, since we are done with all the basics of the peek operation, we will understand the code below as well.
int peek(struct stack* sp, int i)
{
int arrayInd = sp->top -i + 1;
if(arrayInd < 0)
{
printf("Not a valid position for the stack\n");
return -1;
}
else
{
return sp->arr[arrayInd];
}
}
stackTop, stackBottom & Time Complexity of Operations in Stack Using Arrays
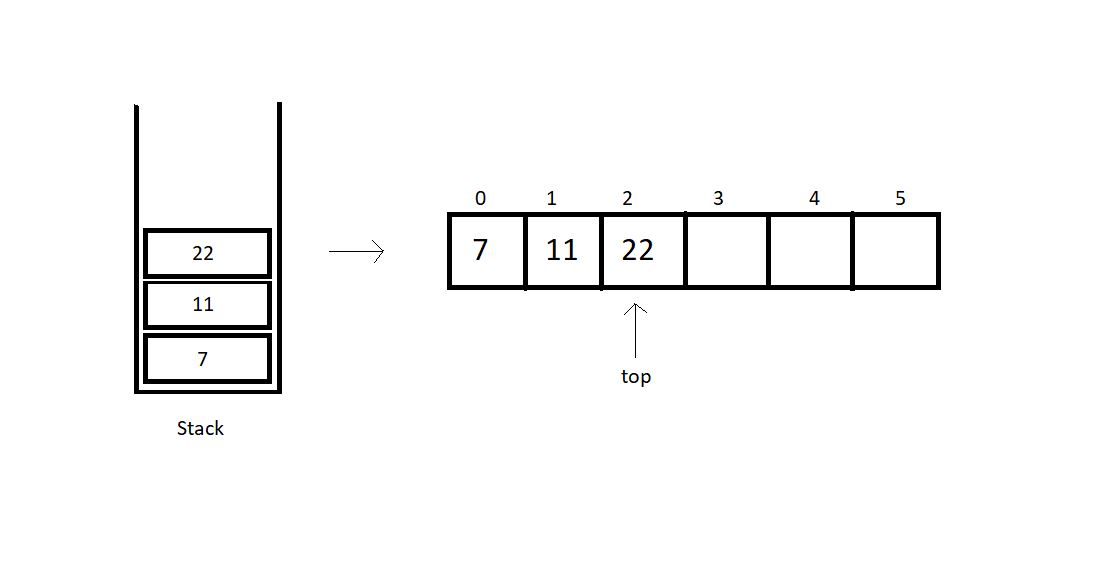
stackTop:
This operation is responsible for returning the topmost element in a stack. Retrieving the topmost element was never a big deal. We can just use the stack member top to fetch the topmost index and its corresponding element. Here, in the illustration above, we have the top member at index 2. So, the stackTop operation shall return the value 22.
Create an integer function stackTop, and pass the reference to the stack you created as a parameter. Just return the element at the index top of the array. code is below:-
int stackTop(struct stack* sp)
{
return sp->arr[sp->top];
}
stackBottom:
This operation is responsible for returning the bottommost element in a stack, which intuitively, is the element at index 0. We can just fetch the bottommost index, which is 0, and return the corresponding element. Here, in the illustration above, we have the bottommost element at index 0. So, the stackBottom operation shall return the value 7.
Create an integer function stackBottom, and pass the reference to the stack you created as a parameter. And then return the element at the index 0 of the array.
int stackBottom(struct stack* sp)
{
return sp->arr[0];
}
One thing one must observe here is that both these operations happen to work in a constant runtime, that is O(1). Because we are just accessing an element at an index, and that works in a constant time in an array.
Time complexities of other operations:
isEmpty(): This operation just checks if the top member equals -1. This works in a constant time, hence, O(1).
isFull(): This operation just checks if the top member equals size -1. Even this works in a constant time, hence, O(1).
push(): Pushing an element in a stack needs you to just increase the value of top by 1 and insert the element at the index. This is again a case of O(1).
pop(): Popping an element in a stack needs you to just decrease the value of top by 1 and return the element we ignored. This is again a case of O(1).
peek(): Peeking at a position just returns the element at the index, (top - position + 1), which happens to work in a constant time. So, even this is an example of O(1).
So, basically all the operations we discussed follow a constant time complexity.
Implement Stack Using Linked List
stacks using linked lists:
We can now consider a singly linked list. Follow the illustration below.
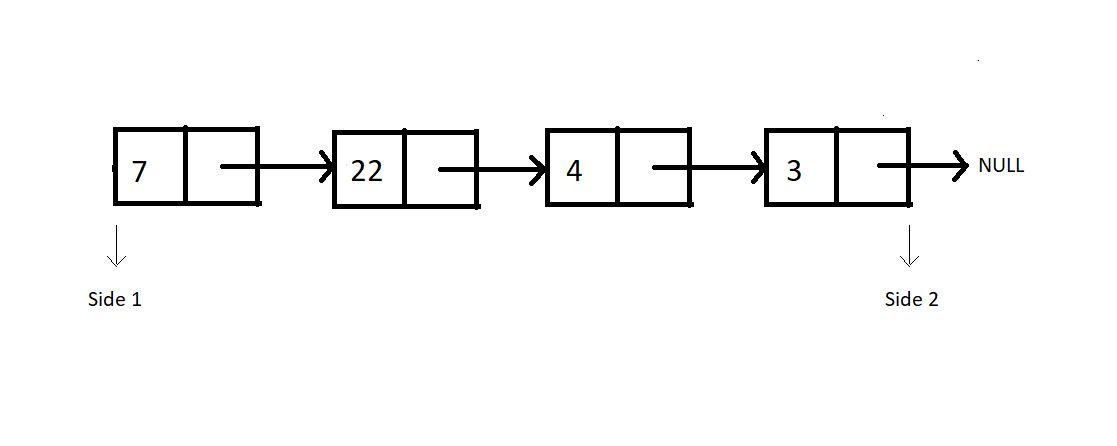
Consider this linked list functioning as a stack. And as you know, we have two sides of a linked list, one the head, and the other pointing to NULL. Which side do you feel should we consider as the top of the stack, where we push and pop from the head side.
And why the head side, that is side 1?
Because that’s the head node of the linked list, and insertion and deletion of a node at head happens to function in a constant time complexity, O(1). Whereas inserting or deleting a node at the last position takes a linear time complexity, O(n).
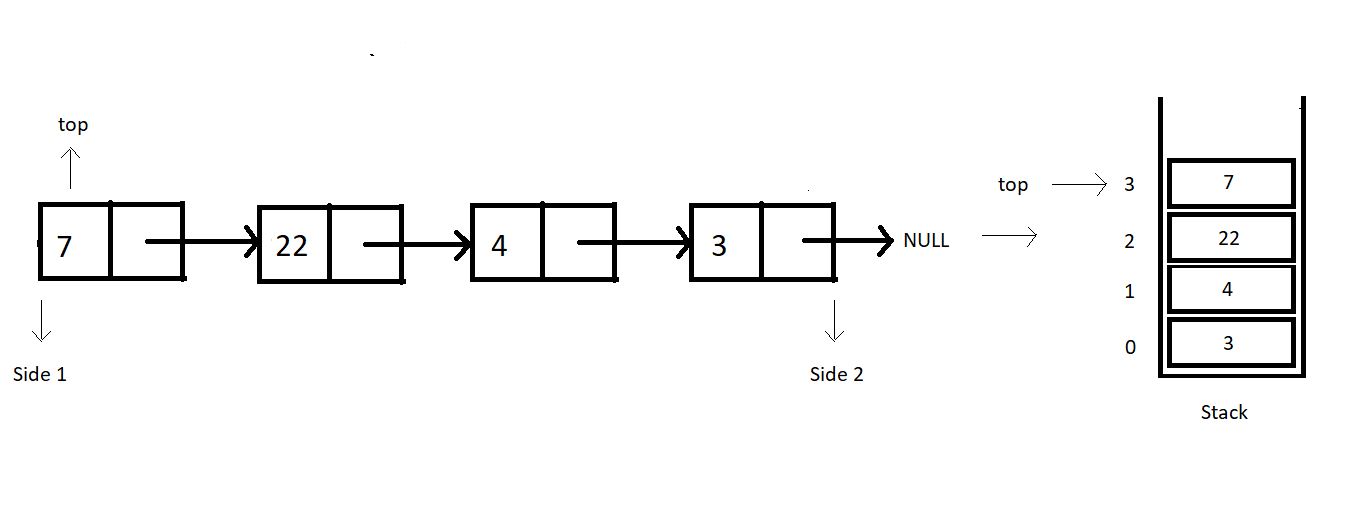
So that stack equivalent of the above illustrated linked list looks something like this:
Let’s revise how we used to define a struct Node in linked lists. We had a struct, and two structure members, data and a struct Node pointer to store the address of the next node.
struct Node
{
int data;
struct Node* next;
}
Structure of a Node in a Linked List
When is our stack empty or full?
Stacks when implemented with linked lists never get full. We can always add a node to it. There is no limit on the number of nodes a linked list can contain until we have some space in heap memory. Whereas stacks become empty when there is no node in the linked list, hence when the top equals to NULL.
Condition for stack full: When heap memory is exhausted
Condition for stack empty: top == NULL
One change I would like to implement before we proceed; the head node we had in linked lists, is the top for our stacks now. So, from now on, the head node will be referred to as the top node.
Even though a stack-linked list has no upper limit to its size, you can always set a custom size for it.
Implementing all the Stack Operations using Linked List
1. isEmpty : It just checks if our top element is NULL.
2. isFull : A stack is full, only if no more nodes are being created using malloc. This is the condition where heap memory gets exhausted.
3. Push : The first thing we need before pushing an element is to create a new node. Check if the stack is not already full. Now, we follow the same concept we learnt while inserting an element at the head or at the index 0 in a linked list. Just set the address of the current top in the next member of the new node, and update the top element with this new node.

4. Pop : First thing is to check if the stack is not already empty Now, we follow the same concept we learnt while deleting an element at the head or at the index 0 in a linked list. Just update the top pointer with the next node, skipping the current top.
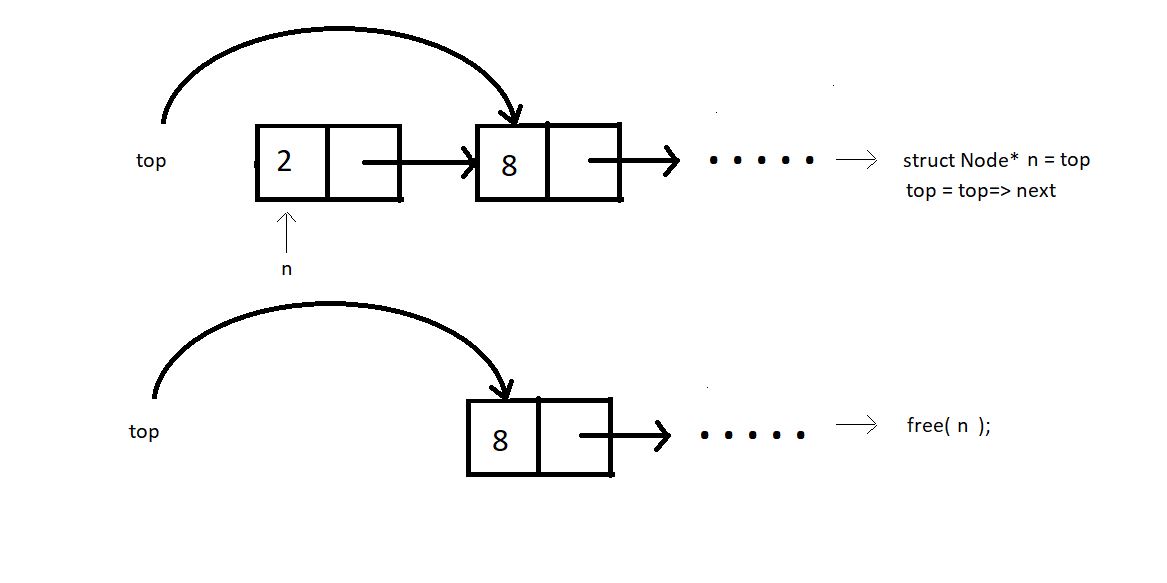
Understanding the code below:
isEmpty():
Create an integer function isEmpty, and pass the pointer to the top node as the parameter. If this top node equals NULL, return 1, else 0.
int isEmpty(struct Node* top){
if (top==NULL){
return 1;
}
else{
return 0;
}
}
isFull():
Create an integer function isFull, and pass the pointer to the top node as the parameter.
Create a new struct Node* pointer p, and assign it a new memory location in the heap. If this newly created node p is NULL, return 1, else 0.
int isFull(struct Node* top){
struct Node p = (struct Node)malloc(sizeof(struct Node));
if(p==NULL){
return 1;
}
else{
return 0;
}
}
Push():
Create a struct Node* function push which will return the pointer to the new top node.
We’ll pass the current top pointer and the data to push in the stack, in the function.
Check if the stack is already not full, if full, return the condition stack overflow.
Create a new struct Node* pointer n, and assign it a new memory location in the heap.
Assign top to the next member of the n structure using n-> next = top, and the given data to its data member.
Return this pointer n, since this is our new top node.
struct Node push(struct Node top, int x){
if(isFull(top)){
printf("Stack Overflow\n");
}
else{
struct Node n = (struct Node) malloc(sizeof(struct Node));
n->data = x;
n->next = top;
top = n;
return top;
}
}
Pop() :
Create an integer function pop which will return the element we remove from the top.
We’ll pass the reference of the current top pointer in the function. We are passing the reference this time, because we are not returning the updated top from the function.
Check if the stack is already not empty, if empty, return the condition stack underflow.
Create a new struct Node* pointer n, and make it point to the current top. Store the data of this node in an integer variable x.
Assign top to the next member of the list, by top = top->next, because this is going to be our new top.
Free the pointer n. And return x.
int pop(struct Node** top){
if(isEmpty(*top)){
printf("Stack Underflow\n");
}
else{
struct Node n = top;
top = (top)->next;
int x = n->data;
free(n);
return x;
}
}
peek(), stackTop() and Other Operations on Stack Using Linked List
peek: This operation is meant to return the element at a given position. Do mind that the position of an element is not the same as the index of an element. In fact, there is nothing as an index in a linked list. Refer to the illustration below.
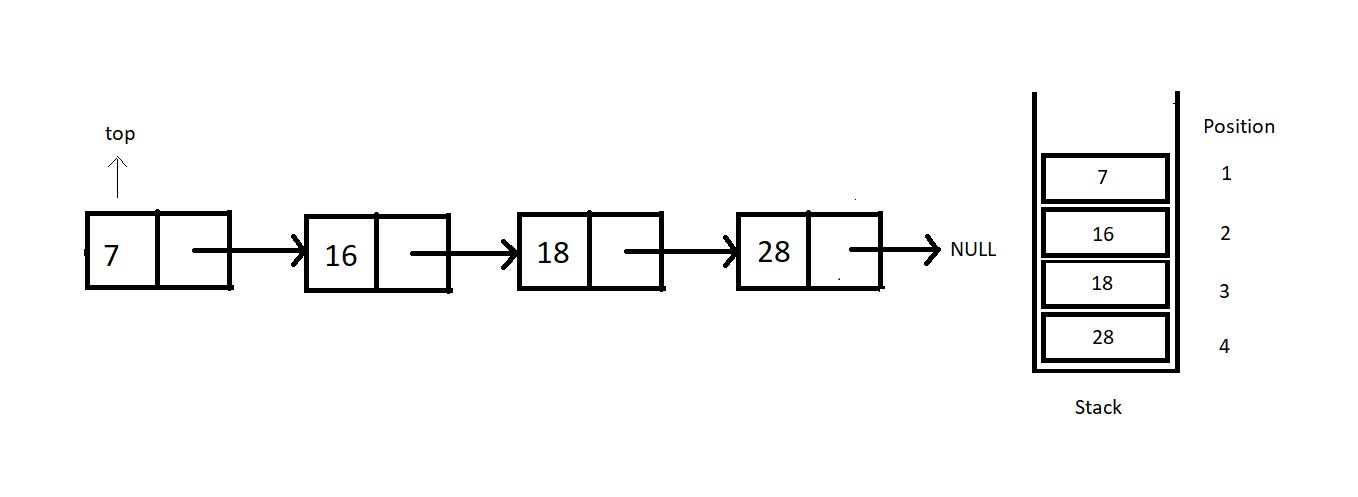
Peeking in a stack linked list is not as efficient as when we worked with arrays. Peeking in a linked list takes O(n) because it first traverses to the position where we want to peek in. So, we’ll just have to move to that node and return its data.
Create an integer function peek, and pass the position you want to peek in as a parameter.
Since we have made the stack pointer global, we should not use that pointer to traverse; otherwise, we will lose the pointer to the top node. Rather create a new struct Node pointer ptr and give it the value of top.
Run a loop from 0 to pos-1, since we are already at the first position.
If our pointer reaches NULL at some point, we must have reached the last node, and the position asked was beyond the available positions, hence breaking the loop.
If the current pointer found the position and it is not equal to NULL, return the data at that node, else -1.
int peek(int pos){
struct Node* ptr = top;
for (int i = 0; (i < pos-1 && ptr!=NULL); i++) {
ptr = ptr->next;
}
if(ptr!=NULL){
return ptr->data;
}
else{
return -1;
}
}
2. stackTop: This operation just returns the topmost value in the stack. That is, it just returns the data member of the top pointer.
Create an integer function stackTop, and we are no longer passing any parameter since the top pointer is declared globally.
Simply return the data member of the struct Node pointer top, and that’s it.
int stackTop(){
return top->data;
}
3. stackBottom: This operation just returns the bottom value in the stack. That is, it just returns the data member of the bottom pointer.
int stackBottom (struct Node*top) {
struct Node*ptr=top;
while (ptr->next!=NULL) {
ptr=ptr->next;
}
return ptr->data;
}